聊聊凯利公式

生活记录投资LY2025-04-142025-04-26

经典案例

以抛硬币为例子，正反概率都是0.5，即概率为：
$$
p = q =1/2
$$
理论上说，如果没有爆仓，每次投入资金都一样，那么一直投，最终会是不亏不赚，总资产基本没多大变化。

具体而言，假设我们初始资产是X_0,X_n表示n次下注后我们的资产，每次下注B_K，用T_K = 1表示第k次下注获胜，用T_k = -1表示下注失败，对于上述符合，对于所有k >= 1,都有：

$$
X_{k} = X_{k-1} + T_{k}B_{k}
$$

引入初始资金，进一步可以得到：

$$
X_{n} = X_{0} +\sum^{n}_{k=1}T_kB_k
$$

进一步得到：
$$
E(X_n) = X_0 + \sum^n_{k=1}E(T_kB_k) = X_0+\sum^n_{k=1}(p-q)E(B_k)
$$
对于抛硬币，p = q= 1/2，即：
$$
E(X_{n}) = X_{0}
$$

当p > q，即胜率大于输率，这个时候，如果要让E(X_{n})最大，就需要最大化每次E(B_{k})，所以这种情况，需要把全部资产全部下注，然后总资产随着次数增加就会几何数级增长
p < q，即胜率小于输率，如果要让E(X_{n})最大，就需要最小化每次E(B_{k})，这种情况，我们不需要投注，每次B_K = 0,这样就可以保证资产不变，E(X_{n}) = X_{0}

比例投注

在上述基础上，我们每次下注时，会按照一定比例去下注，也就是存在一个参数：
$$
0 <= f <= 1
$$
使得：
$$
B_{i} = fX_{i-1}
$$
也就是说，每次投注的时候，基于上一轮的总资产来投注相应的比例即可，如果当前资产时X，下注赢了，总资产为X(1 + f)，如果输了,则为X(1 - f)，那么进行了n次下注，有如下：
$$
X_n = X_0*(1+f)^S*(1-f)^F
$$

S，F分别表述成功和失败次数，且Ｓ＋Ｆ＝ｎ

ｆ＝０，表示不下注
ｆ＝１，表示每次全部下注，只要Ｆ＞＝１，就会出现Ｘｎ＝０，即归零，如果运气好，s=n，f=0，Xn＝X0*2^n
０＜ｆ＜１：

$$
lnX_n = lnX_0 + S*ln(1+f)+F*ln(1-f)
$$

$$
G_n (f) =ln(X_n/X_0)^{1/n}
$$
$$
(lnX_x - lnX_0)/n = (S/n)ln(1+f)+(F/n)ln(1-f)
$$
进一步可得：
$$
g(f) = E(ln(X_n/X_0)^{1/n})
$$

$$
E((S/n)ln(1+f) + (F/n)ln(1-f))
$$

$$
pln(1+f)+qln(1-f)
$$
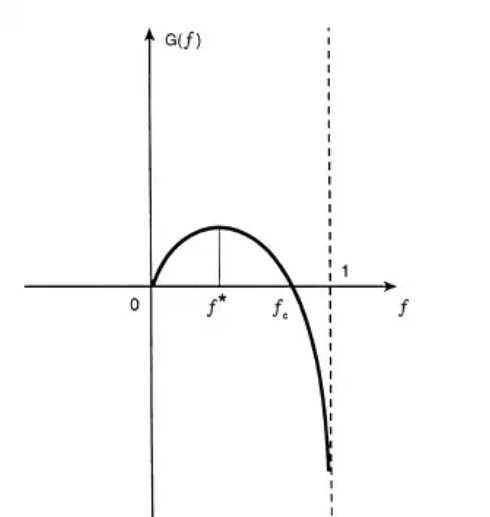
所以可以通过研究g(f)来确定E(Xn)最大值，当p,q在0~1区间:
$$
g(0) = lim_{f->1}-f(f) = -\infty
$$
求导：
$$
Dg(f) = \frac{p}{1 + f} - \frac{q}{1-f} = \frac{p-q-f}{1-f^2}
$$

$$
D^2g(f) = \frac{-(1-f)^2-4fq}{(1-f^2)^2} < 0
$$
Dg(f)是个严格递减函数：

f < p-q时，Dg(f)>0
f < p-q时，Dg(f)<0

因此g(f)会在：
$$
f^* = p-q
$$
取最大值。

因此，如果p<q，那么最好不要下注，输概率大，如果p>q,投注最佳比例为p-q,这个情况下，可以得到:
$$
g(f^*) = plnp+ qlnq+ln2
$$
存在一个fc使得g(fc) = 0

一般形式1

赢钱的时候需要考虑赔率，押1赔b，这就是赢钱率，资产从1增加到1+b，举个例子：当硬币有偏差，同时有赔率的时候，该怎么办？

这个情况下，g(f)可以有如下形式：
$$
g(f) = pln(1 + bf) + qln(1-f)
$$
p、q分别表示赢钱和输钱概率，p+q = 1，f表示下注比例，且0<= f <= 1,可以有如下：
$$
Dg(f) = \frac{pb - q- bf}{(1+bf)(1-f)}
$$
g(0) = 0,且：
$$
lim_{f->1^-} - g(f) = -\infty
$$